14 Page Rank

Il Page Rank è un algoritmo di link analysis che assegna un peso numerico ad ogni elemento di un insieme di documenti collegati da hyperlink

14.1 Flow formulation

Il Web può essere rappresentato come un grafo in cui i nodi sono le pagine e gli archi sono i link tra le pagine. Il PageRank di una pagina viene definito ricorsivamente e dipende dal numero di link entranti, cioè dal numero di pagine che si riferiscono ad essa (non da quelli uscenti, altrimenti una pagine si boosterebbe da sola collegandosi a tantissime pagine), e dal PageRank di queste pagine, maggiore è il PageRank di una pagina con link entrante, tanto maggiore sarà l’aumento del PageRank della pagina citata.

Ogni voto di un link è proporzionale all’importanza della pagina sorgente. Pertanto, se la pagina p con importanza r_p ha n link uscenti, ogni suo voto vale \dfrac{r_p}{n} , mentre la sua importanza è data dalla somma dell’importanza dei voti ricevuti: r_p = \displaystyle \sum_{i \rightarrow p} \dfrac{r_i}{n_i}, dove i è la generica pagina che cita p e n_i è il numero di link uscenti dalla pagina i. Considerando quindi un grafo con n nodi, otterremmo n equazioni a n incognite, per garantire che ci sia una soluzione unica si impone che la somma dei voti sia pari a 1, aggiungendo questa nuova equazione. Questi sistemi però sono infeasible per il Web, in cui gli n nodi sono tantissimi.

14.2 Matrice di adiacenza stocastica

Una riformulazione più computabile è fornita dalla rappresentazione in forma di matrice di adiacenza stocastica.

Dato un qualsiasi grafo la sua matrice di adiacenza è matrice binaria quadrata che ha come righe e colonne i nomi dei vertici del grafo. L’entrata (i, j) della matrice vale 1 se e solo se esiste nel grafo un arco che va dal vertice i al vertice j, 0 altrimenti.

Una matrice di adiacenza stocastica è una matrice di adiacenza in cui una cella può avere un valore compreso tra 0 e 1.

Per costruire la matrice di adiacenza stocastica M, sia i una pagina con d_i link uscenti, se i \rightarrow j, allora M_{ji} = \dfrac{1}{d_i} altrimenti M_{ji} = 0. M, a meno di dead ends, è una matrice stocastica per colonna, ovvero una matrice le cui colonne hanno somma 1. Dato r un vettore con un valore per ogni pagina: r_i è l’importanza della pagina i. La somma dei valori di r è 1: \displaystyle \sum_i r_i = 1 Con questa rappresentazione il vettore dei rank r deriva dal prodotto della matrice di adiacenza stocastica per il vettore stesso. Pertanto dato r = M \cdot r, possiamo dire che r è l’autovettore di autovalore 1 per M, la cui esistenza è garantita dalla stocasticità, pertanto r può essere efficientemente calcolato applicando il metodo delle potenze.

14.2.1 Metodo delle potenze

Il metodo delle potenze è un metodo iterativo per il calcolo approssimato dell’autovalore di modulo massimo di una matrice e il corrispondente autovettore.

Si fissa un vettore di partenza, le cui entrate valgono \dfrac{1}{N}, con N il numero delle pagine, e lo si moltiplica iterativamente alla matrice.

Il criterio di stop è dato dalla differenza norma uno dei due vettori inferiore ad un certo \epsilon:

Vettore iniziale: r_0 = [1/N, …, 1/N]^{T}

Passo iterativo: r_k = M \cdot r_{k - 1}

Criterio di stop: |r_{k+1} - r_{k}|_1 < \epsilon

14.3 Random Walk

Alla base dell’interpretazione con Random Walk vi è l’idea che il PageRank possa essere valutato calcolando la probabilità di raggiungere una pagina da una qualsiasi altra pagina.

Immaginiamo un random web surfer che al tempo t si trova sulla pagina i, al tempo t + 1 segue in maniera stocastica un link uscente da i che lo conduce sulla pagina j.

Sia p(t) il vettore la cui i-esima entrata è la probabilità che il navigatore sia sulla pagina i al tempo t, allora p(t) rappresenta una distribuzione di probabilità sulle pagine.

Pertanto, stabilire su quale pagina si trovi il navigatore a tempo t + 1 è sufficiente risolvere l’equazione p(t + 1) = M · p(t).

Se supponiamo che il random walk raggiunga uno stato in cui p(t + 1) = M · p(t) = p(t), allora p(t) è una distribuzione stazionaria della random walk, indipendente dal vettore di distribuzione iniziale.

14.4 Problemi di convergenza

La convergenza del metodo non è garantita. Vi sono due casi che potrebbero portare il vettore del PageRank a non convergere: lo spider trap e il dead end

14.4.1 Problemi di convergenza: spider trap

Per spider trap si intende la situazione in cui un gruppo di pagine ha link uscenti solo in pagine appartenenti allo stesso gruppo, facendo rimbalzare tra di esse l’importanza complessiva e creando un loop che, in un certo senso, imprigiona il web surfer.

La soluzione allo spider trap è dato dal random teleport, un’assunzione per cui il web surfer può raggiungere qualsiasi pagina p del web a prescindere dal nodo in cui si trova, come se utilizzasse una barra di ricerca di un browser.

Pertanto, ad ogni step, il random surfer ha due opzioni: con probabilità \beta segue un link, con probabilità 1 - \beta si teletrasporta randomicamente.

14.4.2 Problemi di convergenza: dead end

Il problema del dead end consiste nell’avere una pagina senza link uscenti. Quindi un web surfer che finisce in una pagina senza link uscenti vi ci resta bloccato. Questo fa si che la probabilità che il navigatore visiti una qualsiasi altra pagina sia 0.

La soluzione al dead end è l’always teleport. L’assunzione è equivalente a quella fatta per lo spider trap, in questo caso il surfer dovrà necessariamente saltare su un’altra pagina con probabilità 1.

14.4.3 Garantire la convergenza

A questo punto, per garantire la convergenza, si rende necessario rendere la matrice M:

stocastica aggiungendo dei link fittizi in modo che tutte le colonne sommino ad 1, come se creassimo dei link fittizi per i nodi che non rendono la matrice stocastica dal singolo nodo verso se stesso e tutti gli altri
aperiodica aggiungendo un link fittizio da ogni nodo verso se stesso
irriducibile, aggiungendo un link fittizio tra tutti i nodi

Questo viene fatto attraverso la seguente equazione:

r_j = \displaystyle \sum_{ i \rightarrow j} \beta \dfrac{r_i}{d_i} + (1 - \beta) \dfrac{1}{n}

quindi, con probabilità \beta il surfer segue un link, con probabilità 1 - \beta salta su una pagina randomica.

Matrice di Google: A = \beta \cdot M + (1 - \beta) \dfrac{1}{n} I, con I matrice identità.

14.4.3.1 Una matrice di Google

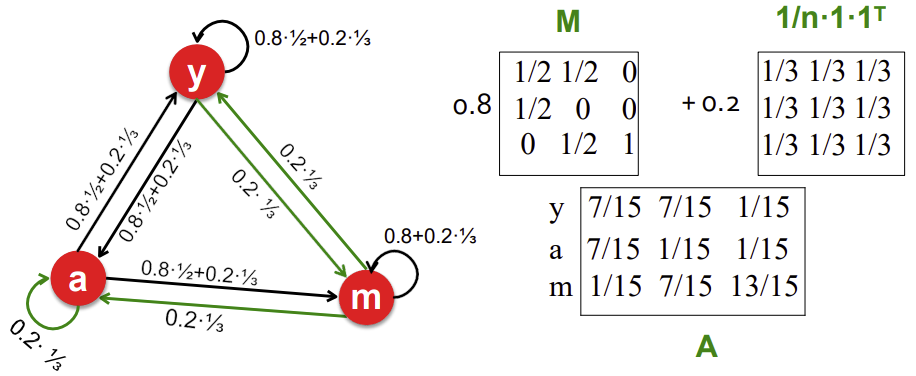
Attenzione: la matrice di Google è applicabile solo su matrici senza dead ends

Matrice già stocastica: tabella e basta
Matrice non stocastica per Dead End: Always Teleport
- Se chiede di renderla aperiodica, irriducibile e stocastica: matrice di Google su matrice già aggiustata con Dead End